Transmission line power flow is an integral part of power systems studies and is used to calculate steady state voltage, voltage angle, real and reactive power flow in an interconnected power system. Interconnected power system will have many generators, loads and interconnecting transmission lines.

Key parameter engineers evaluate while performing power flow studies is voltage stability. Operating beyond the maximum permissible real or reactive power load can cause voltage stability issues leading to voltage collapse and system wide blackouts. Power flow calculations assume load kVA (S) to be constant or varying slowly. Relation between load kVA and bus voltage is expressed by a set of equations known as power flow equations which are non-linear equations that has to be solved iteratively. Power flow studies are also known as load flow studies. This article discusses the simple problem of AC power flow and voltage stability in AC transmission lines.
Read: Surge impedance loading of transmission line
Consider two generators connected via a short transmission line as shown in figure 1. Complex power (S= P + jQ) transmitted and received can be written as equation 1 below:
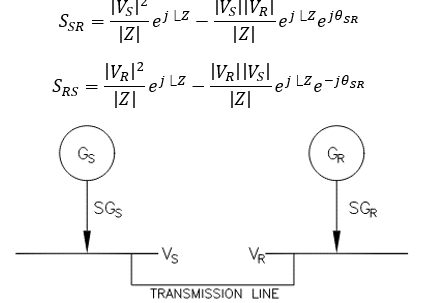
For short lines, line resistance is small and can be ignored compared to inductance. Under this condition, power flow equations can be re-written as equation 2 below:
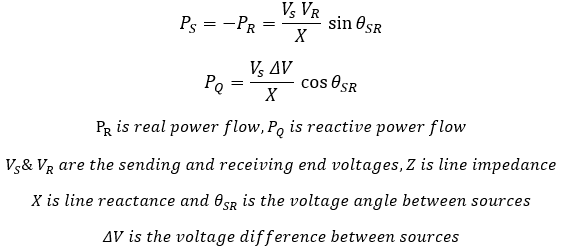
Calculator below illustrates the concept.
Following observation can be made from reviewing equations 1 and 2:
- For a given length of transmission line (Z= fixed), complex power sent or received depends on VS, VR and θSR.
- VS and VR varies with the field current injected in to the sending and receiving end generators.
- θSR is determined by difference of mechanical power inputs to both generators. Real power flows if there is angle difference between voltage on either end of transmission line. Real power flows to the bus that has a lagging angle compared to reference bus.
- Under normal conditions, sending and receiving end voltages are kept within pre-set limits whereas θSR is varied considerably. Difference of mechanical input power determines the power exchange in this case.
- For a line that has finite resistance, ultimate limit for received power is when θSR=⎿Z. When θSR is increased beyond the ultimate transmission capability, the generators will go ‘out of step’ or go out of ‘synchronism’. Typically, the angle is limited to < 300 due to stability considerations.
- For an ideal lossless line, ultimate limit for active power occurs when θSR =90 degree where equation 2 reduces to PR= VS VR/X. Typically, the angle is limited to < 300 due to stability considerations.
- Ultimate transmission capacity (PR) can be increased by increasing VS, VR and by decreasing X. Line inductance X can be decreased by conductor bundling or other methods.
- Reactive power (Var) flows only if there is a difference of bus voltage. Reactive power flows from a bus that has higher voltage to a bus that has lower voltage on per unit basis.

Under normal conditions, sending and receiving end voltages are held fairly close (VS = VR). Lines will be predominantly inductive meaning ⎿Z=900. And θSR will be always less than 30 degrees and often less than 10 degrees. Under these conditions, there will be good decoupling between the active and reactive power where active power couples strongly with θSR and reactive power couples strongly with VS-VR. In other words, active power exchange is strongly dependent on mechanical power input and reactive power exchange is strongly dependent on field current input.
Read: Voltage regulation
Power System Stability
Power system stability is basically voltage stability and is the ability of a power system to maintain steady voltage at all buses in the system after being subjected to a disturbance from a given initial operating condition. Unstable power system can lead to voltage collapse. IEEE defines voltage collapse as “the process by which the sequence of events accompanying voltage instability leads to a blackout or abnormally low voltages in a significant part of the power system.” In an unstable condition, voltage drop caused due to power flow is no longer in the order of few percent as is typical but suffers from drastic voltage swings.
Power system stability can be broadly classified as two: Angle stability and Voltage stability.
Read: Voltage unbalance
Angle Stability
Consider a generator feeding a load as shown in figure 2. Power delivered to load is given by:
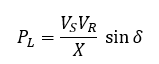
Power delivered to load varies as sine of the angle difference between source and load. As the angle difference increases from zero to 90 degrees, power delivered increases and reaches a maximum. Further increase in angle leads to reduced power transfer.
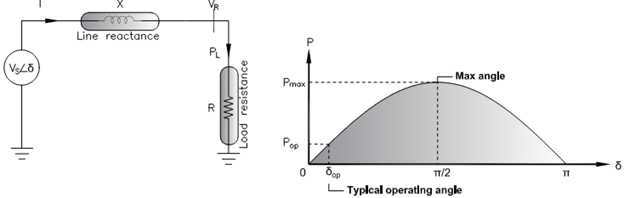
Typical operating angle is less than 30 degrees. Any power system disturbance can cause synchronous generator rotor angle to swing widely, potentially crossing the maximum stable angle of 90 degree. For this reason, operating angle is kept safely away from the maximum angle.
Read: Voltage tolerance standard- ANSI C84.1
Voltage Stability
Consider a simple two bus system as shown in figure 3. Current flowing in the circuit is:
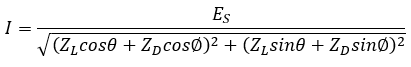
Receiving end voltage and power drawn by load can be written as:
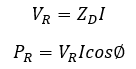
As the load impedance is decreased keeping the load power factor (𝞍) same, real and reactive power consumption is increased. As the load impedance decreases, current increases, terminal voltage VR decreases. This will continue till a maximum power point or knee point after which any further decrease in load impedance (i.e., increased load) will result in drop of terminal voltage and eventually the real power consumed by load starts to decrease. Knee point is where the system will reach maximum tolerable voltage difference between source and load. Normalized values of voltage, current and power are shown in figure 4.
Read: Voltage swell due to line-ground fault
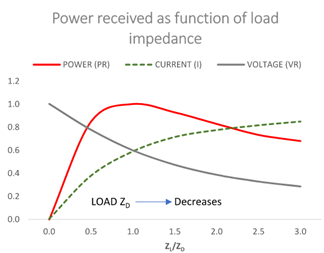
As the load is increased (load impedance ZD is decreased), power is increased rapidly at first and then slows down before reaching a maximum point. There is a thus a maximum amount of power that can be transmitted through an impedance from a given voltage source.
Maximum power is transmitted when receiving end voltage (VR) is equal to line voltage drop. This occurs when load impedance ZD is equal to line impedance ZL (maximum power transfer theorem).
Read: Charging current in high voltage cable
P-V Curve for Stability Analysis
Voltage stability can be analyzed using P-V curve which shows the interaction between power delivered at a constant power factor and the corresponding change in bus voltage. Power requirement at a bus is increased in steps and corresponding bus voltage is measured. P-V curve graphically plots the maximum power that may be transmitted between two parts of the power system before voltage collapse. P-V curves are also known as nose curves.
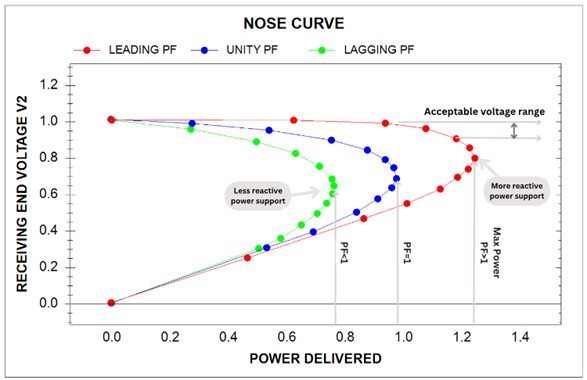
As the power delivered is increased, the curve starts at top left corner. Receiving end voltage gradually decreases until the ‘tip’ of the nose curve which is the maximum power that can be delivered to this load (assuming sufficient reactive power is available). Past the ‘tip’ of the curve, further increase in load power causes both power and voltage to decrease as it follows the bottom portion of curve. At the collapse point, even a slight increase in power demand will decrease bus voltage drastically. Curve also illustrates the advantage of operating with unity or leading power factor.
Read: AC voltage drop and system power factor
Intuitively the P-V curve may be difficult to grasp. Consider figure 6 with an ideal generator, line resistance and a resistive load to understand the basic idea. As the load resistance is decreased, load current and power consumed in load increases. However, at some high value of load current, line resistance now starts to consume more power compared to load. Line resistance now creates more voltage drop causing load terminal voltage and load power to drop.
Read: Source impedance calculation in power systems
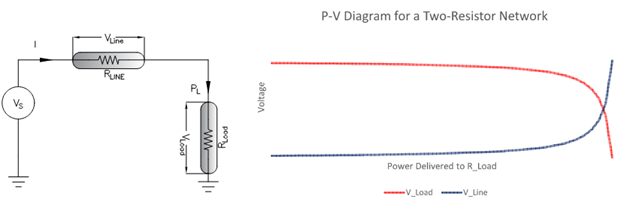
Above is a simple network and hence the concept is easy to visualize. In a practical power system comprising of generators, line and load impedances, the power flow parameters are more complex and involves solutions to quadratic equations.
Read: Cold load pickup in power distribution networks
Q-V Curve for Stability Analysis
Q-V curves are used to analyze voltage stability with respect to reactive power injection. Reactive power requirement at a bus is increased in steps and corresponding bus voltage is measured. Q-V curve graphically plots the maximum reactive power that may be transmitted between two parts of the power system before voltage collapse.
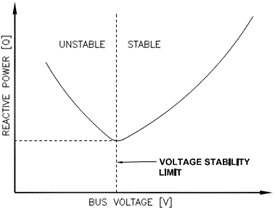
The point at which the rate of change of reactive power with voltage is zero is the voltage stability limit. Stable region in the figure is what we would typically expect- Increasing bus voltage with increasing reactive power injection. Providing sufficient reactive power close to the load is critical in maintaining power system voltage stable.
