Sequence Components

What are positive, negative, zero sequence components in power system and how do you calculate them?

Three phase electric power system voltage, current can be mathematically reduced to three distinct sets of symmetrical sequence components; positive, negative and zero sequence for both voltage and current.

When we refer to sequence (symmetrical) components, it is important to remember that sequence components always refer to line-neutral or line-ground quantities. Sequence component and symmetrical component refers to the same material.

Use the calculator below as negative sequence current calculator, zero sequence current calculator or positive sequence current calculator. Input the three phase voltage/current and their corresponding phase angles (in degrees) and the calculator will provide the positive, negative and zero sequence voltage/current magnitude. Note that the calculator is based on ABC phase rotation. See how ABC phase rotation looks like in the picture below.

If you input ACB phase sequence instead of ABC sequence in to the calculator, the results of positive and negative sequence values will be interchanged. The values will still be correct.

Per convention positive direction of angle measurement is counterclockwise.

Sequence Voltage Calculator

Sequence Current Calculator

Positive sequence consists of balanced three phase voltage and current phasors which are exactly at 120 degrees apart rotating counterclockwise in ABC rotation. Remember voltages are line-neutral. This is the voltage that we can expect out of an ideal three phase generator.

Negative sequence consists of balanced three phase voltage and current phasors which are exactly at 120 degrees apart rotating counterclockwise in ACB rotation.

Zero sequence consists of balanced three phase voltage and current, phasors of which all have same phase angles and rotate counterclockwise together.

Considering power system phase sequence of a-b-c, positive sequence components are all of same magnitude, rotating counter clockwise in the order of a-b-c. Remember power system phasors always rotate in counter clockwise direction. See article on phase sequence and phase angle if you would like to know more about power system phase rotation.

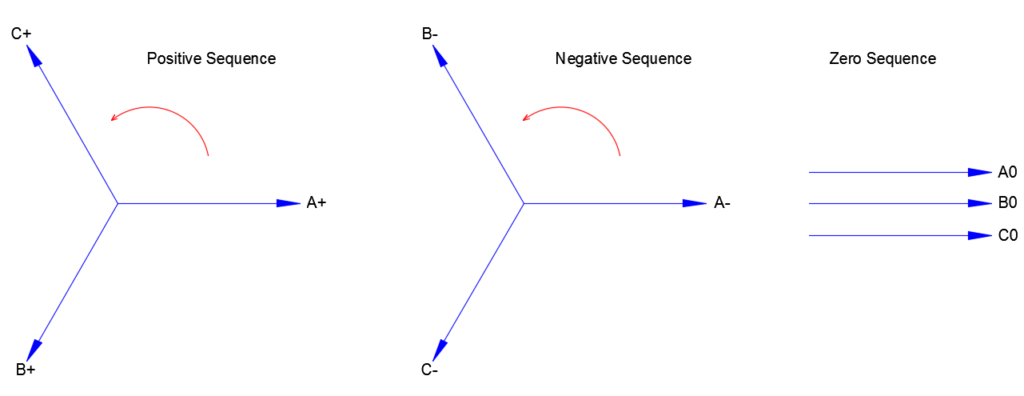
Positive, Negative, Zero Sequence Components

Lets define ‘a’ as a unit phasor with 120 degree phase angle displacement. Thus,

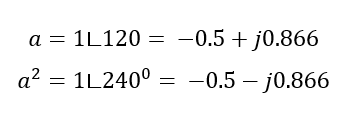
The relation between three phase voltage V_a, V_b, V_c and the sequence components V₀, V₁, V₂ is given by the following equation:

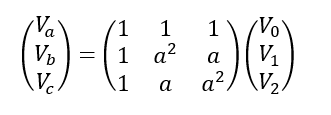
From this equation, the sequence voltage components can be calculated to be:

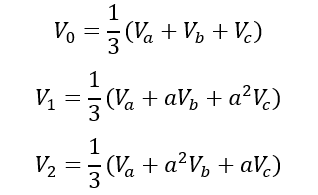
Similarly, the sequence current components are:

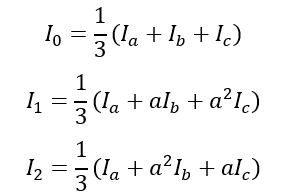
Here V₀,I₀ is the zero sequence component V₂, I₂ is the negative sequence component, V₁,I₁ is the positive sequence component. The calculator above uses these formulas to calculate the sequence component.

Properties and uses of sequence components

Positive Sequence Components

All generators, power system sources ideally should only generate positive sequence voltages. Thus, the magnitude of positive sequence voltage establishes how good a source is.
A balanced three phase system will only have positive sequence components. No negative or zero sequence components will be present.
All modern microprocessor based relays use positive sequence current for overcurrent protection. Negative sequence overcurrent is a separate optional element and has to be enabled if necessary in most relays.
Positive sequence quantities are used in voltage and current unbalance calculation specifically in true unbalance equation.

Negative Sequence Components

Negative sequence voltage creates negative sequence current in motors that creates flux in the opposite direction to the positive sequence flux. This will cause additional heating in motor.
Negative sequence is used in directional relaying and unbalance protection.
Negative sequence overcurrent protection is available as option in most modern microprocessor based relays.
A balanced three phase system with will not have any negative or zero sequence components.
Negative sequence quantities are used in voltage and current unbalance calculation specifically in true unbalance equation.

Zero Sequence Components

Zero sequence current is important in ground fault current calculations.
From the equation for zero sequence current above, it can be seen that the neutral current (sum of I_a, I_b, I_c) is three times the zero-sequence current (3I₀). This principle is used in ground fault detection of grounded neutral systems by connecting three current transformers on the three phase lines in parallel.
From the equation for zero sequence voltage above, it can be seen that adding three phase voltages (sum of V_a, V_b, V_c) is three times the zero-sequence voltage (3V₀). This principle is used in ground fault detection of ungrounded systems by connecting three voltage transformers in broken delta.
In a balanced Y-connected system (with neutral ungrounded) the line current cannot have any zero sequence components since the neutral current is zero.
In a balanced delta-connected system the line current cannot have any zero sequence components, however zero sequence currents can circulate in the closed delta winding.
A balanced three phase system will not have any negative or zero sequence components.
Though we can define a term called zero sequence voltage unbalance, it is not very useful practically. Hence you will not see the term zero sequence voltage unbalance used much.

Sequence Components and Harmonics

Harmonic voltages and currents have interesting relation with sequence component theory. All harmonic voltages and currents belong to either positive, negative or zero sequence component. It follows the rules established for sequence current flow in the power system.

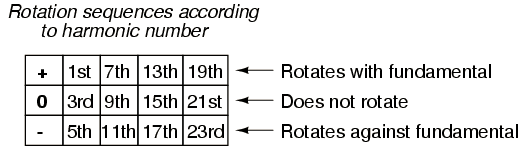
Fundamental frequency balanced voltage or current will only have positive sequence components
Third harmonic (3*60Hz or 3*50Hz) currents behave like zero sequence component
Fifth harmonic is similar to negative sequence
Seventh harmonic is similar to positive sequence
Ninth harmonic is similar to zero sequence
Eleventh harmonic is similar to negative sequence
Thirteenth harmonic is similar to positive sequence
Fifteenth harmonic is similar to zero sequence
Seventeenth harmonic is similar to negative sequence
Nineteenth harmonic is similar to positive sequence
Twenty-first harmonic is similar to zero sequence
Twenty-third harmonic is similar to negative sequence

Here is a summary of the sequence components and corresponding phase sequence from 1^st through 23^rd. This knowledge is important when troubleshooting power quality issues, unbalance or ground current problems.

Harmonic Frequency and Rotation Sequence Calculator

Another way to understand sequence components is to understand how they behave in wye and delta systems.

Three phase wye connected systems: Fundamental, 5^th, 7^th, 11^th, 13^th, 17^th , 19^th, 23^rd etc. harmonics can flow in the three-phase system without a neutral conductor or ground return. The 3^rd, 9^th, 15^th , 21st etc. harmonics can flow only when a ground or neutral return exists.

Three phase Delta systems: 5^th, 7^th, 11^th, 13^th, 17^th , 19^th, 23^rd etc. harmonics can flow in the lines, however 3^rd, 9^th and 15^th etc. harmonics can flow inside the delta winding in a closed loop and not on the lines.

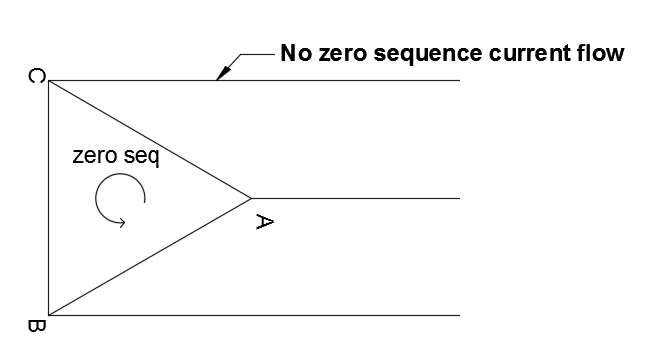
The topic of zero sequence current flow in three phase transformers requires careful study of the type of winding connection, type of transformer, type of transformer core etc. This will be a topic for a future article.