In this article wye (star) and delta connection is discussed with respect to line-line, line-neutral voltages and currents. Additionally, the vector phase angles between delta and wye connection is also discussed.
WYE connection- Voltage
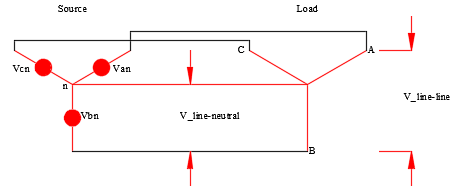
For WYE connection, the source neutral is connected to the load neutral. Even if there is there is no neutral wire, but the source neutral and the load neutral is grounded (earthed) the same discussions apply. If the source and load neutrals and ungrounded, the voltages would be the same as with grounded neutral EXCEPT when there is fault in the system. When there is a line-ground fault on a wye-ungrounded source, voltages will become unbalanced. When there is a line-ground fault on a wye-grounded source, voltages will be balanced for the most part.
For this discussion let’s assume the line-neutral source voltages are as follows:
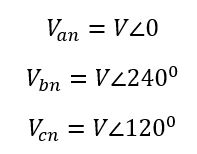
The line to neutral load voltage at the wye connected load will be the same as above.
However, the line-line (phase-phase) voltage at the load will be given by:
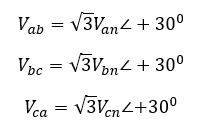
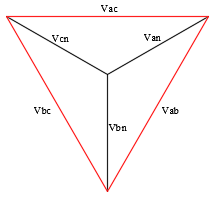
That means in a three-phase wye-grounded system with positive sequence voltages, the line-line voltage is √3 times the line-neutral voltage and leads by 300. The vector diagram below represents this magnitude and phase angle change.
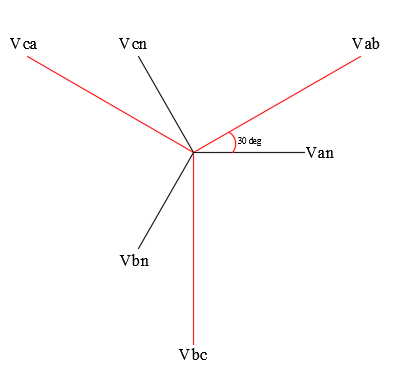
Following important points to be noted:
Line-Neutral Voltage: For a balanced system, the sum of line-neutral voltages (Van +Vbn +Vcn) is zero. For unbalanced voltage, this sum will not be zero and will result in the zero sequence neutral voltage and result in neutral current flow if the neutrals are connected together.
Line-Line Voltage: For a balanced or unbalanced system, the sum of line-line voltages (Vab +Vbc +Vca) is zero. This is because the line-line vectors form a closed triangle and even if one of the voltage magnitude is reduced, the other voltages readjust to form a closed triangle.
WYE connection- Current
For a wye connected load with wye connected source, line currents are balanced with 1200 displacement between any two phases. Line currents and load current will be equal.
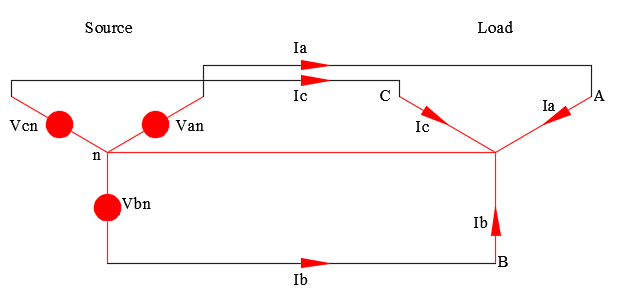
For a wye connected load, neutral current is calculated by adding the following vectorially. This means both magnitude and phase angle need to be considered.
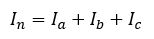
For balanced three phase currents, the sum of Ia +Ib +Ic will be zero. Even if the impedance on the neutral connection is varied from 0 to ∞ the neutral current will be zero provided the system is balanced. If the system is not balanced neutral current will flow between neutral points of source load and source.
DELTA connection- Voltage
For a delta connected load, the source line-line voltage and the delta connected load line-line voltages will be the same. Even though there is no neutral for a delta system, an imaginary neutral at the centroid of the delta triangle can be assumed. When the system is balanced, this imaginary neutral and the source neutral will be at the same ground potential. Hence when the delta is balanced, the line-ground potential at the load is same as the source line-neutral voltage. When there is a line-ground fault on the delta system (system becomes unbalanced), the voltages to ground are not the same.
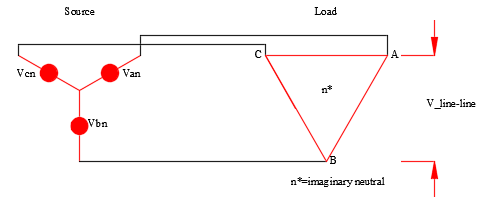
DELTA connection- Current
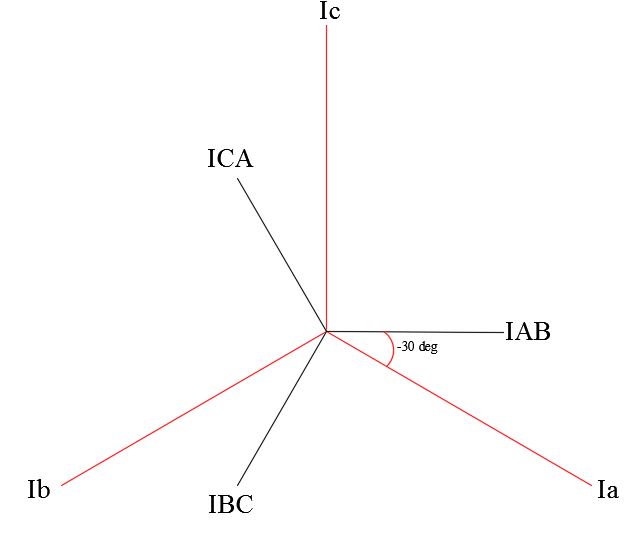
The figure below shows a wye connected source feeding a balanced delta connected load. The line currents in this case is given by:
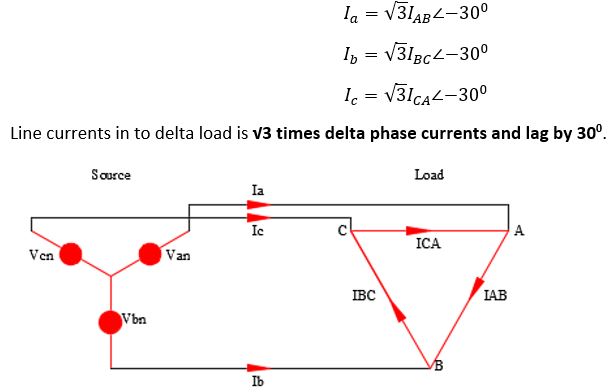
For balanced three delta load currents, the sum of IAB +IBC +ICA will be zero. If the delta load impedances are not balanced, then the phase currents (IAB, IBC etc) will not be balanced. However even in this case the sum of line currents (Ia+Ib+Ic) will be zero since there is no neutral wire.
Additional Reading:
Transformer Connections: Phase Shift and Polarity
